「ぼーっとしてるね。」
「ヨーロッパ旅行の話やっと終わったしね。」
「気が抜けてる感じじゃない?」
「気候のせい?」
ちがうちがう。
考え事してるんだ。
宇宙の果てまで点が行ったらどうなるだろうかって。
「それって、ずっと前に三角形の窓の話の時に言ってたこと?」
そうそう、よく覚えてるじゃない。
「訳が分らなかったってことだけ覚えてる」
でさー、今年の年賀状に楕円が円に見える写真を出したって前に話したじゃない?それで、また楕円のこと考えてる。
「また〜!」
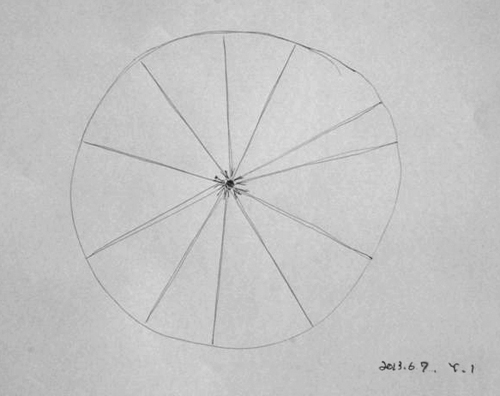
円は中心に点が一つあって、
中心からもしボールを円周上に作った壁に投げたとしたら、
壁に当たってまた円の中心に戻って来るんだ。
円の中心に立っていればどこに投げても自分に戻ってくる。
まるで、ピッチャー返し!
「そんなことわざあったような?」
どんな?
「天に向かってつばを吐けば、必ず自分に降って来るって。」
だねー、そんな感じかも。
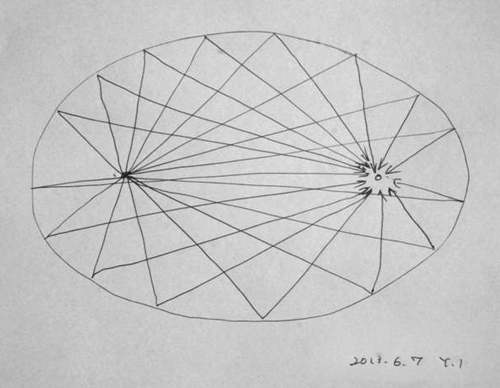
それで、楕円になったら、今度は中心が二つになる。
そして、一つの中心からボールを投げると、
必ずもう一つの中心にやって来る。
どこに向かって投げても、もう一つの中心にやって来る。
あいてが、それをよけると今度は最初の中心に集まる。
「不思議だね。」
放物線、って知ってる?
ボールなどを投げ上げたときに山なりになって落ちてくるけど、
その形。二次関数なんて言い方もするけど。
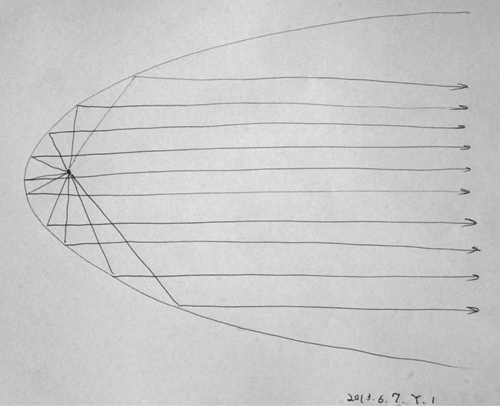
放物線にも中心があって、
中心から投げかけられたものはすべて中心軸に平行に進んでいく。
逆にいえば、平行にやってきたものは
すべて中心に集まる。
だから、パラポラアンテナなんて言って、
お皿の形をしたものをレーダーの受信アンテナに使ったり、
衛星放送のアンテナだったり、
鳥の鳴き声や虫の鳴き声など、
かすかな音を録音するときに使う集音マイクだったり。
そうそう、いわゆる凹面鏡って呼ばれている鏡はすべてこの形。
反射式の望遠鏡の鏡もね。
そういえば、確かギリシャのオリンピアで灯される
オリンピックの聖火も確か、太陽の光をこの反射鏡で集めていると思う。
「それで、何考えてるの?いったい?」
そう、前の話で、頂点が永遠の彼方に行った
二等辺三角形の斜辺は平行になるじゃない。
放物線って、ひょっとしたら
もう一つの中心点が永遠の彼方に行ったんじゃないかなって、
考えてるんだ。
一つの中心点から投げられたものは、
放物線の壁に当たってもう一つの中心である
永遠の点に向かって進んでいるんじゃないかなって。
だから、放物線も楕円のなかまじゃないかってね。

でさあ、そうしたら双曲線も楕円の仲間に出来ないだろうかって…
「確か、曲線が2本あるやつ?」
そう、そう
「2本の線をどうやって、一つの輪と同じと考えることができるの?」
「屁理屈を使うしかないような。」
考えれば考えるほど、ぼーっとするね。
